του Πολ Λόκχαρτ1
Διαβάστε το 1ο μέρος εδώ: Ο Θρήνος του μαθηματικού (μέρος 1o)
Μαθηματικά και Πολιτισμός
Το πρώτο πράγμα που έχουμε να καταλάβουμε είναι ότι τα μαθηματικά είναι μια τέχνη. Η διαφορά ανάμεσα στα μαθηματικά και στις άλλες τέχνες, όπως η μουσική και η ζωγραφική, είναι ότι ο πολιτισμός μας δεν τα αναγνωρίζει σαν τέτοια. Όλοι αντιλαμβάνονται ότι οι ποιητές, οι ζωγράφοι και οι μουσικοί δημιουργούν έργα τέχνης, και ότι εκφράζονται μέσα από λέξεις, εικόνες και ήχους. Πράγματι, η κοινωνία μας είναι αρκετά γενναιόδωρη όσον αφορά στη δημιουργική έκφραση· αρχιτέκτονες, μάγειρες, ακόμα και σκηνοθέτες της τηλεόρασης θεωρούνται καλλιτέχνες. Επομένως, γιατί όχι και οι μαθηματικοί;
Μέρος του προβλήματος είναι ότι κανείς δεν έχει την παραμικρή ιδέα του τι κάνουν οι μαθηματικοί. Η κοινή αντίληψη φαίνεται να είναι πως οι μαθηματικοί συνδέονται κατά κάποιο τρόπο με την επιστήμη· ίσως βοηθούν τους επιστήμονες με τους μαθηματικούς τους τύπους, ή τροφοδοτούν υπολογιστές με μεγάλα νούμερα για τον έναν ή τον άλλο λόγο. Δεν υπάρχει αμφιβολία πως, αν ο κόσμος έπρεπε να χωριστεί σε «ονειροπόλους ποιητές» και σε «ορθολογικούς στοχαστές», τότε οι περισσότεροι άνθρωποι θα τοποθετούσαν τους μαθηματικούς στη δεύτερη κατηγορία.
Παρόλα αυτά, είναι γεγονός ότι δεν υπάρχει τίποτα τόσο ονειρικό και ποιητικό, τίποτα τόσο ριζοσπαστικό, ανατρεπτικό και ψυχεδελικό όσο τα μαθηματικά. Το καθετί στα μαθηματικά είναι τόσο συναρπαστικό όσο η κοσμολογία ή η φυσική (οι μαθηματικοί αντιλήφθηκαν τις μαύρες τρύπες πολύ πριν οι αστρονόμοι βρουν κάποια), και επιτρέπει μεγαλύτερη ελευθερία έκφρασης απ’ ό,τι η ποίηση, οι τέχνες ή η μουσική (οι οποίες εξαρτώνται σε μεγάλο βαθμό από τις ιδιότητες του υλικού σύμπαντος). Τα μαθηματικά είναι η πιο γνήσια των τεχνών, όπως και η πιο παρεξηγημένη.
Έτσι, ας προσπαθήσω να εξηγήσω τι είναι τα μαθηματικά και τι κάνουν οι μαθηματικοί. Δεν υπάρχει καλύτερος τρόπος απ’ το να ξεκινήσω με τη θαυμάσια περιγραφή του Γκ. Χ. Χάρντι:
Ο μαθηματικός, όπως ο ζωγράφος ή ο ποιητής, είναι δημιουργός μοτίβων2. Αν τα μοτίβα του είναι πιο μόνιμα από των άλλων δύο, αυτό συμβαίνει γιατί φτιάχνονται με ιδέες.
Επομένως, οι μαθηματικοί κάθονται φτιάχνοντας μοτίβα ιδεών. Τι είδους μοτίβα; Τι είδους ιδέες; Ιδέες σχετικά με τους ρινόκερους; Όχι, αυτούς τους αφήνουμε στους βιολόγους. Ιδέες σχετικά με τη γλώσσα και τον πολιτισμό; Συνήθως όχι. Όλα τα παραπάνω είναι πάρα πολύ πολύπλοκα για το γούστο των περισσότερων μαθηματικών. Αν υπάρχει κάτι σαν μια ενωτική αρχή καλαισθησίας είναι αυτό: το απλό είναι όμορφο. Οι μαθηματικοί απολαμβάνουν να σκέφτονται για τα απλούστερα πιθανά πράγματα, και τα απλούστερα πιθανά πράγματα ανήκουν στη φαντασία.
Για παράδειγμα, αν έχω διάθεση να σκεφτώ σχήματα –και συνήθως έχω– θα μπορούσα να φανταστώ ένα τρίγωνο που βρίσκεται μέσα σε ένα ορθογώνιο κουτί:

Αναρωτιέμαι πόσο χώρο καταλαμβάνει το τρίγωνο μέσα στο κουτί. Τα δύο-τρίτα ίσως; Αυτό που είναι σημαντικό να καταλάβουμε είναι ότι δεν μιλάω γι’ αυτό το σχέδιο τριγώνου μέσα σε ένα κουτί. Ούτε μιλάω για κάποιο μεταλλικό τρίγωνο που αποτελεί μέρος συστήματος δοκών μιας γέφυρας. Δεν υπάρχει κάποιος ανώτερος πρακτικός σκοπός εδώ. Απλά παίζω. Αυτό είναι και τα μαθηματικά, το να περιπλανιέσαι, να παίζεις, να διασκεδάζεις με τη φαντασία σου. Πρώτα απ’ όλα, το ερώτημα πόσο χώρο καταλαμβάνει το τρίγωνο μέσα στο κουτί δεν έχει νόημα για πραγματικά, φυσικά αντικείμενα. Ακόμα και το πιο προσεκτικά κατασκευασμένο φυσικό τρίγωνο παραμένει μια απελπιστικά πολύπλοκη συλλογή κινούμενων ατόμων· το μέγεθός του αλλάζει από λεπτό σε λεπτό. Έτσι είναι, εκτός κι αν θέλουμε να μιλήσουμε για κάποιου είδους προσεγγιστικές μετρήσεις. Λοιπόν, εδώ είναι που μπαίνει η αισθητική. Αυτό σίγουρα δεν είναι απλό, και συνεπώς πρόκειται για ένα άσχημο ερώτημα που εξαρτάται από κάθε είδους λεπτομέρειες του φυσικού κόσμου. Ας το αφήσουμε στους επιστήμονες. Η μαθηματική ερώτηση είναι σχετικά με ένα φανταστικό τρίγωνο που είναι εγγεγραμμένο σε ένα φανταστικό κουτί. Οι πλευρές του είναι τέλειες επειδή έτσι θέλω να είναι, αυτό είναι το είδος του αντικειμένου που προτιμώ να εξετάσω. Αυτό είναι ένα μείζον θέμα στα μαθηματικά: τα αντικείμενα είναι ότι εσύ θες να είναι. Έχεις απεριόριστες επιλογές, η πραγματικότητα δεν μπλέκεται στα πόδια σου.
Απ’ την άλλη πλευρά, από τη στιγμή που έχεις κάνει τις επιλογές σου (για παράδειγμα μπορεί να επιλέξω να κατασκευάσω ένα συμμετρικό τρίγωνο, ή και όχι) τότε οι νέες σου δημιουργίες κάνουν αυτό που κάνουν, είτε σου αρέσει είτε όχι. Αυτό είναι το εκπληκτικό του να φτιάχνεις φανταστικά πρότυπα: σου αντιμιλάνε! Το τρίγωνο καταλαμβάνει συγκεκριμένη επιφάνεια του κουτιού, κι εγώ δεν έχω κανέναν έλεγχο πάνω στο ποια είναι αυτή η επιφάνεια. Υπάρχει ένας αριθμός κάπου εκεί, ίσως είναι δύο-τρίτα, ίσως πάλι όχι, αλλά δεν μπορώ να πω ποιος είναι. Πρέπει να τον ανακαλύψω.
Έτσι ξεκινάμε να παίζουμε και να φανταζόμαστε ό,τι θέλουμε και να φτιάχνουμε μοτίβα και να θέτουμε ερωτήσεις σχετικές μ’ αυτά. Αλλά πώς απαντάμε αυτές τις ερωτήσεις; Δεν μοιάζει καθόλου με επιστήμη. Δεν υπάρχει κανένα πείραμα που να μπορώ να κάνω με δοκιμαστικούς σωλήνες, εξοπλισμό και ούτω καθεξής που θα μου πει την αλήθεια για ένα επινόημα της φαντασίας μου. Ο μόνος τρόπος για να φτάσουμε στην αλήθεια σχετικά με τις φαντασίες μας είναι να χρησιμοποιήσουμε τις ίδιες τις φαντασίες μας, κι αυτό είναι σκληρή δουλειά.
Στην περίπτωση του τριγώνου μέσα στο κουτί του, παρατηρώ κάτι απλό και όμορφο:
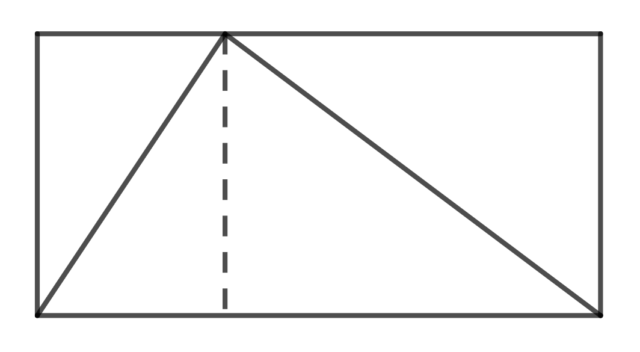
Αν χωρίσω το ορθογώνιο σε δυο κομμάτια όπως στο σχήμα, βλέπω πως κάθε κομμάτι κόβεται στη μέση διαγώνια από τις πλευρές του τριγώνου. Έτσι όσος χώρος υπάρχει μέσα στο τρίγωνο άλλος τόσος υπάρχει κι έξω από αυτό. Αυτό σημαίνει ότι το τρίγωνο πρέπει να καταλαμβάνει ακριβώς το μισό κουτί!
Αυτά βλέπει κι αισθάνεται κάποιος που καταπιάνεται με τα μαθηματικά. Αυτή η μικρή αφήγηση είναι ένα παράδειγμα της τέχνης των μαθηματικών: το να κάνουμε απλές και κομψές ερωτήσεις σχετικά με τα δημιουργήματα της φαντασίας μας και να δημιουργούμε ικανοποιητικές και όμορφες εξηγήσεις. Πράγματι, δεν υπάρχει τίποτα άλλο που να μοιάζει εντελώς με αυτή την περιοχή των καθαρών ιδεών· είναι συναρπαστικό, έχει πλάκα και είναι ελεύθερο!
Τώρα, από πού μου ήρθε αυτή η ιδέα; Πώς ήξερα να ζωγραφίσω αυτή τη γραμμή; Πώς ξέρει ένας ζωγράφος πού να βάλει το πινέλο του; Έμπνευση, εμπειρία, δοκιμή και σφάλμα, κακοτυχία. Εδώ έγκειται η τέχνη, με το να δημιουργείς αυτά τα όμορφα μικρά ποιήματα σκέψης, αυτά τα σονέτα γνήσιας λογικής. Υπάρχει κάτι τόσο υπέροχα μετασχηματιστικό σ’ αυτή τη μορφή τέχνης. Η σχέση ανάμεσα στο τρίγωνο και στο ορθογώνιο ήταν ένα μυστήριο και στη συνέχεια εκείνη η μοναδική γραμμούλα την έκανε φανερή. Δεν μπορούσα να δω και κατόπιν, ξαφνικά, είδα. Κατάφερα με κάποιο τρόπο να δημιουργήσω μια ουσιαστική, απλή ομορφιά απ’ το τίποτα, και μεταλλάχτηκα μέσα από αυτή τη διαδικασία. Αυτό δεν κάνει και η τέχνη;
Αυτός είναι ο λόγος που είναι τόσο αποκαρδιωτικό να βλέπεις τι γίνεται με τα μαθηματικά στο σχολείο. Αυτή η πλούσια και συναρπαστική περιπέτεια φαντασίας έχει περιοριστεί στην απομνημόνευση ενός συνόλου στείρων “δεδομένων” και διαδικασιών που πρέπει να ακολουθηθούν. Αντί για μια απλή και φυσιολογική ερώτηση σχετικά με τα σχήματα, καθώς και μια δημιουργική και ωφέλιμη διαδικασία εφεύρεσης και ανακάλυψης, οι μαθητές επεξεργάζονται τα εξής:
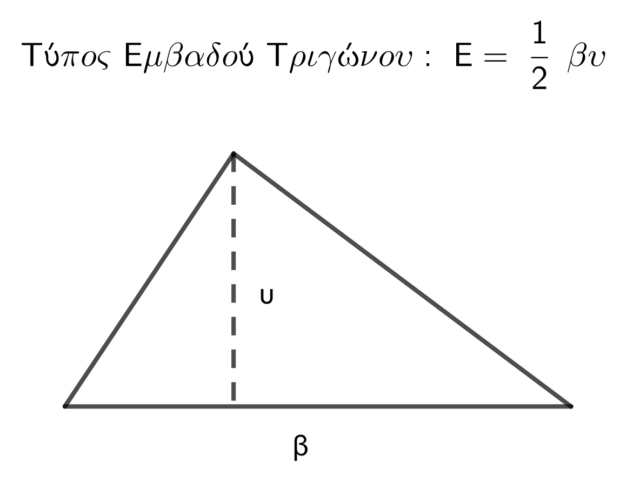
“Το εμβαδόν ενός τριγώνου είναι ίσο με το μισό του γινομένου μιας βάσης του με το αντίστοιχο ύψος”. Ζητείται από τους μαθητές να απομνημονεύσουν αυτόν τον τύπο και στη συνέχεια να τον “εφαρμόσουν” ξανά και ξανά στις “ασκήσεις”. Πάει η συγκίνηση, η χαρά, ακόμα ακόμα και ο πόνος ή η απογοήτευση της δημιουργικής δράσης. Το πρόβλημα πλέον εξαφανίζεται. Η ερώτηση έχει τεθεί και απαντηθεί τη ίδια στιγμή, δεν έχει απομείνει τίποτα στο μαθητή να κάνει.
Διαβάστε το 3ο μέρος εδώ: Ο Θρήνος του μαθηματικού (μέρος 3o)
Μετάφραση* από τα αγγλικά: Νικολέττα Καρασμάνη
Επιμέλεια*: Κώστας Κατσαρός
Η μετάφραση-επιμέλεια, διανέμονται με την άδεια Creative Commons “Αναφορά Δημιουργού – Μη Εμπορική Χρήση – Παρόμοια Διανομή 4.0 Διεθνές (CC BY-NC-SA 4.0)”.

*: Η μετάφραση στα ελληνικά και η επιμέλεια έγινε από μη μεταφραστές και μη επιμελητές. Παρακαλούμε για την ανοχή σας σε τυχόν λάθη. Οποιεσδήποτε παρατηρήσεις είναι, φυσικά, ευπρόσδεκτες.
- Ο Πολ Λόκχαρτ άρχισε να ενδιαφέρεται για τα μαθηματικά όταν ήταν 14 χρονών (έξω από τη σχολική αίθουσα όπως επισημαίνει). Εγκατέλειψε το κολέγιο έπειτα από ένα εξάμηνο για να αφοσιωθεί αποκλειστικά στα μαθηματικά. Βασιζόμενος στη δική του έρευνα, έγινε δεκτός στο Κολούμπια, όπου πήρε το διδακτορικό του, και έχει διδάξει σε σημαντικά πανεπιστήμια, όπως το Μπράουν και αυτό της Καλιφόρνιας (Σάντα Κρουζ). Από το 2000 έχει αφοσιωθεί στην “ανατρεπτική” διδασκαλία των σχολικών μαθηματικών στο Σεντ Ανς Σκουλ στο Μπρούκλιν της Νέας Υόρκης. [↩]
- ΣτΜ: Στο αγγλικό κείμενο “pattern”. Επιλέχθηκε ο όρος “μοτίβο” αντί του μαθηματικά πιο δόκιμου “πρότυπο” για λόγους οικειότητας με το μέσο αναγνώστη. [↩]